Information events

• Before the start of the semester, a pre-course and an information event will take place for our first-year Bachelor students, to which we cordially invite you. For more information on the dates, please refer to the invitation.
• In addition, an orientation event for the elective options in the Bachelor's degree programme is held at the end of the winter semester. The information event "Bachelor specialisation/deepening" took place on Wednesday, 14.04.2023. Information on elective options can be found in B.Sc. Mathematics + Elective Options SoSe 2023. 
• You can find the Online Study Choice Assistant here. You can also find information on all degree programmes under OSA Overview.
• Presentations of past information and orientation events and preliminary courses can be found in the archive.

Start of studies, duration of studies

• The standard period of study is 6 semesters. 
• As a rule, the Bachelor's programme should be started in the winter semester. It is possible to start in the summer semester, but there may be shifts in the study plan." We recommend that you contact the student advisory service if you are unsure about how to begin your studies (Study Regulations (§ 5 (2)).
• Please refer to the course catalogue for times and information on courses. Registration for lectures is not necessary, information on registration for tutorials can be found in the respective lecture. 
• Important: Bachelor's registration form - Please note in the first semester that you must register for the "Bachelor's examination" at the examination office. 

Profile and occupational field of the Bachelor's programme

In the Bachelor's programme, students acquire:

• basic mathematical knowledge in Pure and Applied Mathematics,
• the basic ability to work scientifically,
• methodological competence in a self-selected area of mathematics,
• basic knowledge for the inclusion of computers and electronic media in the implementation or representation of modelling steps,
• the ability to solve a more extensive mathematical problem in a Bachelor's thesis.

Information events

• Invitation to the Master's Orientation Event
• In the week before the winter semester starts, there will be an information and orientation event for first-year Master students.  
• Presentations of past information and orientation events can be found in the archiv.

Start of study, duration of study, prerequisites

• The standard period of study is 4 semesters. The curricula are designed for the start of studies in a winter semester. It is also possible to start the programme in the summer semester; in this case, you should contact the student advisory service to make it easier for you to start the programme.
• The formal requirement is a Bachelor's degree in mathematics or a degree equivalent to a Bachelor's degree in mathematics in another subject. A good knowledge of English is important, because almost all contributions in mathematical research are published in English.
• Important: Master's registration form - Please note in the first semester that you must register for the "Master's examination" at the Examinations Office. 

Intended professional qualification of Master's graduates

In the Master´s programme, students acquire:

• basic mathematical knowledge in Pure and Applied Mathematics,
• the basic ability to work scientifically,
• methodological competence in a self-selected area of mathematics,
• basic knowledge for the inclusion of computers and electronic media in the implementation or representation of modelling steps,
• the ability to solve a more extensive mathematical problem in a Master´s thesis,
• Communication skills

The teacher training program in mathematics qualifies students to teach mathematics at one of the Hessian school types. The Institute of Mathematics is significantly involved in the teacher training courses:

• L1 (Elementary School)
• L2 (Hauptschule and Realschule)
• L5 (special school)
• L3 (grammar school)

The study programs consist of subject-specific and subject-specific didactic parts. In both parts, the study program contains a compulsory and an elective part.

Among the teacher training programs, the subject-specific part is largest in the L3 program. In this program, each student chooses two subjects. The standard duration of the program is nine semesters, including the semester of examinations.

If they choose mathematics as their subject, L3 students take the courses Linear Algebra, Fundamentals of Algebra, Geometry, Analysis 1 in the first three semesters. These courses are offered jointly for the Bachelor of Mathematics and the L3 Mathematics teacher training programs. Due to these joint courses, there is an extensive permeability between the Bachelor's and the L3 studies in the first year of study, which enables the students to reorient themselves between these degrees without any loss of time, if necessary.

The subject-specific academic counselling is aimed at prospective students, students in the introductory phase of their studies, students in part-time studies as well as the specialisation counselling. The Central Student Advisory Service is also available for further concerns. Writing consultations are offered by the Writing Centre at Riedberg.

During your mathematics studies at Goethe University, you have the opportunity to study one or more semesters at a foreign university. For European countries, the ERASMUS programme provides the framework as well as financial and organisational support for your stay abroad. There are also programmes for stays in non-European countries that provide you with organisational support and financial assistance. You can find further information at Global Office of the Goethe-University.

General information on certificates of achievement and module examinations can also be found here.

Representative for Erasmus: apl. Prof. Gaby Schneider

Internationalisation Officer: Prof. Dr. Alex Küronya

General information on studying abroad can be found under the following links:

International Student Service

Orientation events

Invitation from the Dean of Studies

The Fachschaft Mathematik offers an orientation event by students for students, which usually takes place over 7 days before the start of the lecture period. The subject-specific preliminary course is embedded in this event. Participation in the orientation event is voluntary, but attendance is recommended. In addition to information from students about everyday study life and the structure of timetables, you will receive information from the Dean of Mathematics about the structure of the degree programme, the examination regulations and the study regulations. 

You will receive information and an invitation to the mathematics orientation event on the student council homepage.

Please register for this event on the corresponding homepage.

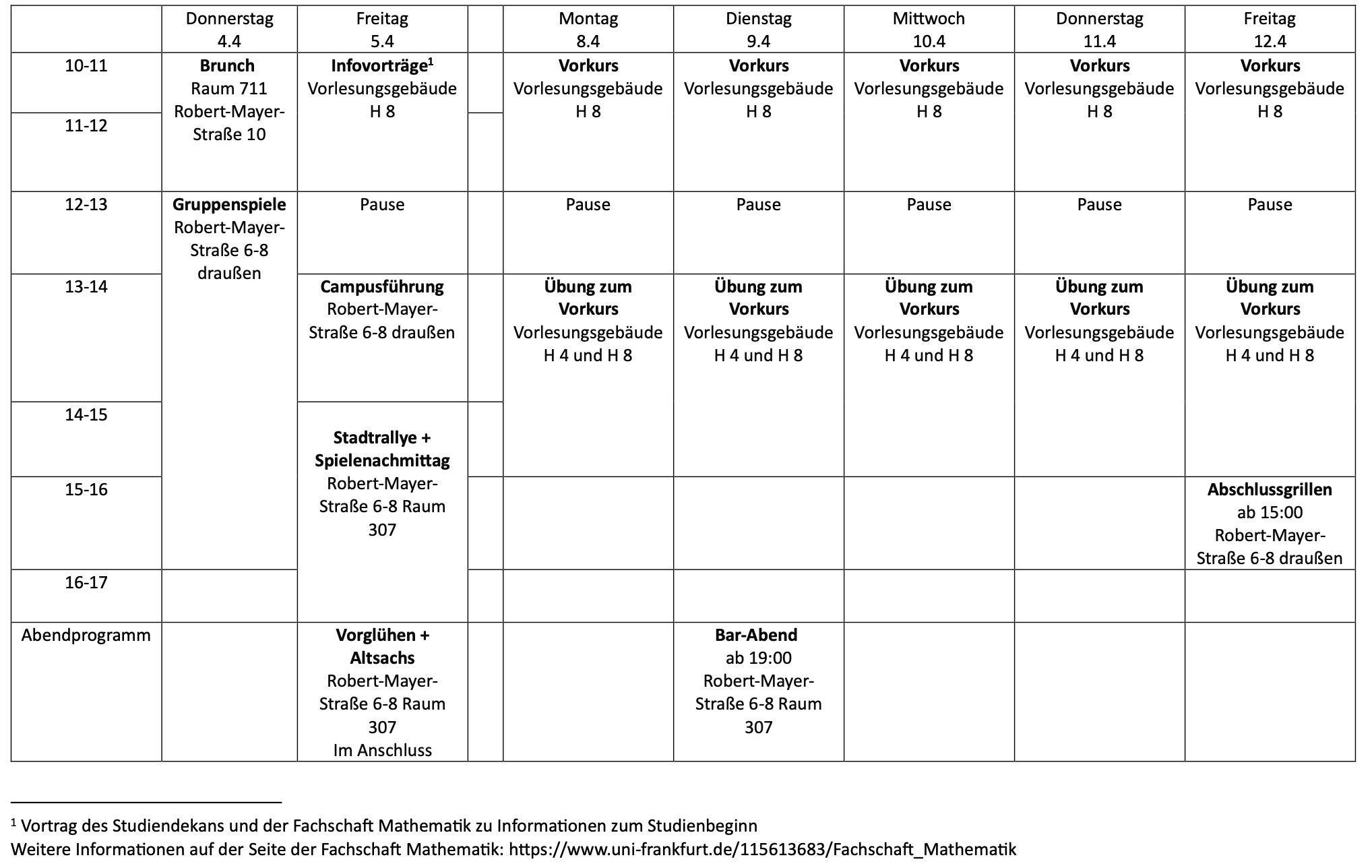
Pre-course

The course is aimed at students of mathematics (B.Sc. and teaching degree) who have no experience with university mathematics. In this course we want to introduce some basic concepts of mathematics that you will encounter in the lectures of the first semester and talk about different principles of proof. We will consolidate what we have learned by means of many exercises, which will be supervised by tutors from higher semesters. In addition, we will discuss various methodological aspects of mathematics studies, e.g. "How do I (effectively) read a mathematical text?" or "How do I approach an exercise?". 

The course will take place in presence. 

Schedule

Time: Monday, 09.10.2023 - Friday, 13.10.2023
Venue: Lecture hall building, Campus Bockenheim, Gräfstraße 50-54, 60325 Frankfurt, Germany 
Room: Lecture: H11 (10:15 - 11:45), Exercises: H11 & H13 (13:15-14:45)
Lecturer: Johannes Horn, horn[at]math.uni-frankfurt.de

Literature

This course largely follows the script by Theresa Kumpitsch from previous semesters. This in turn follows the preliminary course by Sven Jarohs (script) as well as Kerstin Hesse's Introduction to Mathematical Thinking and Working, the Introduction to Mathematical Working by Hermann Schichl and Roland Steinbauer and the Introduction to Mathematical Thinking and Working -- tutorial and transparent by Joachim Hilgert, Max Hoffmann and Anja Panse.

Neither in this course nor in the preliminary courses linked above is school material refreshed. The university's Online Mathematics Bridge Course (OMB+) is a good place to start. Please note that this bridge course is not a preparation for the study of mathematics.

Events of the blue;science university initiative on the topic of mental health in studies.

Mental Health Guide of the blue;science university initiative.

Open consultation hours of the psychosocial counselling service at Goethe University

Telephone councelling
Around the clock at 0800-111-0-111 or 0800-111-0-222

Psychosocial Crisis Service Frankfurt
9 Uhr bis 1 Uhr nachts durchgängig unter 069-611375

Gender Equality Council FB12